 Pomocy :<
Pomocy :<
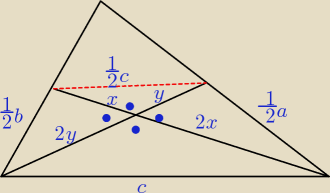 środkowe dzielą się w stosunku 2:1
środkowe dzielą się w stosunku 2:1
| 1 | ||
4x2 +y2 = | a2
| |
| 4 |
| 1 | ||
x2 + 4y2 = | b2
| |
| 4 |
| 1 | ||
x2+y2 = | c2 takie mamy równania, i mamy obliczyć c
| |
| 4 |
| 1 | 1 | |||
4x2 +y2 = | a2 => 4x2= | a2−y2
| ||
| 4 | 4 |
| 1 | 1 | |||
x2 + 4y2 = | b2 => 4y2= | b2−x2
| ||
| 4 | 4 |
| 1 | 1 | ||
a2−y2 + | b2−x2 =c2
| ||
| 4 | 4 |
| 1 | 1 | ||
a2 −(y2 + x2) + | b2 =c2
| ||
| 4 | 4 |
| 1 | 1 | 1 | |||
a2 − | c2 + | b2 = c2 /*4
| |||
| 4 | 4 | 4 |
| √a2+b2*√5 | √5a2+5b2 | |||
c= | = | |||
| 5 | 5 |
| a2+b2 | ||
wynik w odpowiedziach jest bardzo zbliżony √ | ||
| 5 |
 dziękuję bardzo
dziękuję bardzo


 !
!
 ja poprostu usunąłem niewymierność
ja poprostu usunąłem niewymierność
| √a2+b2 | ||
c= | po usunięciu niewymierności otrzymasz to co napisałęm  | |
| √5 |

 winno być chyba tak
winno być chyba tak
| a2+b2 | ||
c2=p{ | ||
| 5 |
| a2+b2 | ||
c=√ | ||
| 5 |
 nie ma potrzeby usuwania niewymiernosci
nie ma potrzeby usuwania niewymiernosci  pamiętaj!
pamiętaj!
| √a | a | ||
= √ | |||
| √b | b |
 1:2 od środka
1:2 od środka 

| a2+b2 | ||
to: √ | , nie wiedziałem czy to bedzie widoczne ze cale wyrazenie jest pod | |
| 5 |
| a2+b2 | √a2+b2 | |||
√ | = |  | ||
| 5 | √5 |
 ok, to daję
ok, to daję  1. (4.133)
W Δ równobocznym ABC poprowadzono wysokość BD i na przedłużeniu wysokości odłożono punkt K, tak
że |BK| = |AC|. Punkt K połączono z punktami A i C. Oblicz |kąt AKC|. Rozważ dwa przypadki.
(Podp.
1. (4.133)
W Δ równobocznym ABC poprowadzono wysokość BD i na przedłużeniu wysokości odłożono punkt K, tak
że |BK| = |AC|. Punkt K połączono z punktami A i C. Oblicz |kąt AKC|. Rozważ dwa przypadki.
(Podp.  1. przyp., gdzie przedłużamy od pkt B, 2. − od pkt D
1. przyp., gdzie przedłużamy od pkt B, 2. − od pkt D  )
2. (n)
W Δ ABC przedłużono bok AB poza wierzchołek B i odłożono odcinek BD równy odcinkowi BC.
)
2. (n)
W Δ ABC przedłużono bok AB poza wierzchołek B i odłożono odcinek BD równy odcinkowi BC.
| |kąt CBA| | ||
Połączono punkty C i D. Wykaż, że |kąt CDA| = | . | |
| 2 |
 w Tobie moja nadzieja
w Tobie moja nadzieja 
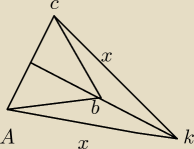 Ad 1 ABK jako trójkąt równoramienny ma kąty przy podstawie równe.
Ad 1 ABK jako trójkąt równoramienny ma kąty przy podstawie równe.
| 1 | a√3 | ||
a2 + ( | + a)2 = x2 =>
| ||
| 2 | 2 |
| 3+2√3 | ||
cosk = | ||
| 4+2√3 |
| β−180o | kąt CBA | |||
kąt BDC = BCD = | => kąt CDA = | |||
| 2 | 2 |
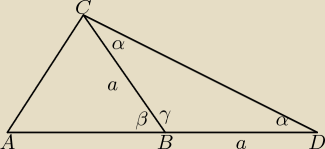 γ=180−2α = 180−β
180−2α = 180−β
2α=β
γ=180−2α = 180−β
180−2α = 180−β
2α=β
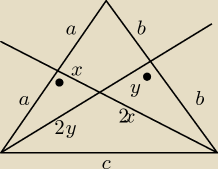 x2+a2 = 4y2 y2+b2 =4x2 c2 =9y2+b2 a2 +9x2 = c2 takie są
równania
podstawimy tak: =>a2 +9x2 = c2 => c2 =9y2 +b2
a2+9x2 = 9y2 + b2 teraz podstawimy to: x2+a2 = 4y2 => a2 = 4y2 −x2
4y2 − x2 +9x2 =9y2 +b2 i teraz y2+b2 =4x2 => b2 = 4x2−y2
4y2 − x2 +9x2 =9y2 +4x2−y2
8x2 +4y2 = 8y2 +4x2
4x2 = 4y2
x=y
skoro to już wiemy to podstawiam za x, y
x2+a2 = 4y2 i y2+b2 =4x2
x2+a2 = 4x2 x2 +b2 = 4x2
a2 = 3x2 b2=3x2 => a=b
teraz wiemy że jest to trójkąt równoramienny a teraz sprawdze czy jest to trójkąt równoboczny
wykorzystam tu to : a2 = 3x2 => a=√3x
cały bok to 2a więc bok to 2√3x
a2 +9x2 = c2
a2 +9x2 =c2
3x2+9x2 = c2
12x2=c2
2√3 x = c
i na tym się kończy
x2+a2 = 4y2 y2+b2 =4x2 c2 =9y2+b2 a2 +9x2 = c2 takie są
równania
podstawimy tak: =>a2 +9x2 = c2 => c2 =9y2 +b2
a2+9x2 = 9y2 + b2 teraz podstawimy to: x2+a2 = 4y2 => a2 = 4y2 −x2
4y2 − x2 +9x2 =9y2 +b2 i teraz y2+b2 =4x2 => b2 = 4x2−y2
4y2 − x2 +9x2 =9y2 +4x2−y2
8x2 +4y2 = 8y2 +4x2
4x2 = 4y2
x=y
skoro to już wiemy to podstawiam za x, y
x2+a2 = 4y2 i y2+b2 =4x2
x2+a2 = 4x2 x2 +b2 = 4x2
a2 = 3x2 b2=3x2 => a=b
teraz wiemy że jest to trójkąt równoramienny a teraz sprawdze czy jest to trójkąt równoboczny
wykorzystam tu to : a2 = 3x2 => a=√3x
cały bok to 2a więc bok to 2√3x
a2 +9x2 = c2
a2 +9x2 =c2
3x2+9x2 = c2
12x2=c2
2√3 x = c
i na tym się kończy to jest trójkąt równoboczny
to jest trójkąt równoboczny
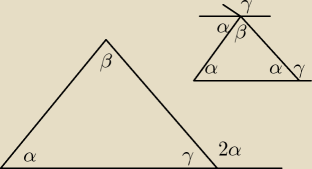 180=α+β+γ
180=2α+γ
α+β+γ=2α+γ
β=α pierwszą część masz
Wykaż, że jeżeli trójkąt jest równoramienny to kąt przyległy do jednego z kątów trójkąta jest
dwa razy większy od drugiego
180=2α+β
180−α=γ
γ=α+β
α+β=180−α
2α+β=180
Odp twierdzenie jest prawdziwe
180=α+β+γ
180=2α+γ
α+β+γ=2α+γ
β=α pierwszą część masz
Wykaż, że jeżeli trójkąt jest równoramienny to kąt przyległy do jednego z kątów trójkąta jest
dwa razy większy od drugiego
180=2α+β
180−α=γ
γ=α+β
α+β=180−α
2α+β=180
Odp twierdzenie jest prawdziwe
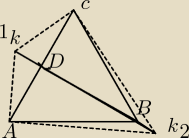 W pierwszym nie o to chodziło zupełnie
W pierwszym nie o to chodziło zupełnie mój rysunek jest taki
k1 to jedna możłiwosc, k2 to druga... i proszę bez funkcji trygonometrycznym!
mój rysunek jest taki
k1 to jedna możłiwosc, k2 to druga... i proszę bez funkcji trygonometrycznym!
 a jeśli chodzi o 4., to w odpowiedziach piszą, że nie jest prawdziwe odwrotne
do reszty nie mam odpowiedzi... proszę o poprawki w 1. i 4.
a jeśli chodzi o 4., to w odpowiedziach piszą, że nie jest prawdziwe odwrotne
do reszty nie mam odpowiedzi... proszę o poprawki w 1. i 4. (wybaczcie, że Was męczę Godzio
i Mateusz)
wierzę, ze 2. i 3. są dobrze
(wybaczcie, że Was męczę Godzio
i Mateusz)
wierzę, ze 2. i 3. są dobrze  DZIĘKUJĘ WAM
DZIĘKUJĘ WAM 
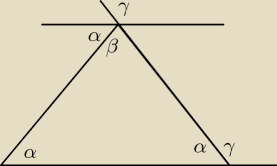 najpierw moje poprawie:
nie wiem kompletnie jak ja to zrobiłem
najpierw moje poprawie:
nie wiem kompletnie jak ja to zrobiłem  jak to nawet wykazane nie jest
założenie : y=2β
γ+α=180 => α=180−γ
γ=α+β
γ=180−γ +β
2γ=180+β
jak to nawet wykazane nie jest
założenie : y=2β
γ+α=180 => α=180−γ
γ=α+β
γ=180−γ +β
2γ=180+β
| 1 | ||
γ=90 + | β
| |
| 2 |
| 3 | |
β=90 czyli trójkąt musiałby być równoboczny, ale że jest równoramienny to się nie zgadza | |
| 2 |

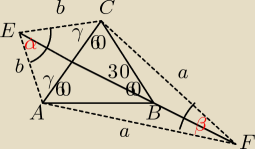 2γ+α=180
trójkąt EBC jest równoramienny
180 −30 =150
150:2=75
czyli : γ+60=75 => γ=15
2γ+α=180
α=150 zaraz 2 przypadek zrobie
2γ+α=180
trójkąt EBC jest równoramienny
180 −30 =150
150:2=75
czyli : γ+60=75 => γ=15
2γ+α=180
α=150 zaraz 2 przypadek zrobie
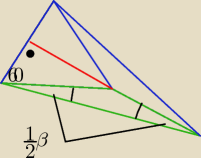 90+60+β=180
β=30
90+60+β=180
β=30
 bo piszę to co napsał mateusz i wychodzi mi, że
bo piszę to co napsał mateusz i wychodzi mi, że
| 180−B | ||
Kąt BDC = Kąt BCD − | ||
| 2 |
| 180−B | B | |||
A że kąt BDC = kąt CDA = | co się nie równa | |||
| 2 | 2 |
 Jesteś mistrzem
Jesteś mistrzem  Oczywiście, nie o było by się bez pomocy Mateusza
Oczywiście, nie o było by się bez pomocy Mateusza  Dziękuję Wam obu
Dziękuję Wam obu 
| B−180 | ||
tzn., napisał | czego nie kumam zupełnie, bo wtedy wyjdzie liczba raczej ujemna, | |
| 2 |
 Już nić
DZIĘKI
Już nić
DZIĘKI !
liczę Godzio na pomoc w przyszłych zadaniach
!
liczę Godzio na pomoc w przyszłych zadaniach 